OpenGL - kamera

Tato kapitola by měla být o tom, jak pohybovat kamerou. Teorii jsem již probral v kapitole o perspektivě (kamera). Praxe je velmi jednoduchá – použijí se jen nějaké funkce z linmath.h, transformují se matice a je hotovo.

Abyste to neměli tak jednoduché, najdete tu ještě jedno téma – jak optimalizovat množství vrcholů potřebných pro vykreslení trojúhelníků sdílejících své vrcholy.

Element array

Podívejte se na následující obrázky. Zobrazují jehlan z předchozí kapitoly, ale navíc také souřadnicové osy. Každá osa je zobrazena pomocí dvou dlouhatánských obdélníků, které jsou navzájem kolmé a tvoří kříž.

Modrá osa je osa z, zelená je x a červená y.

Na prvním obrázku můžete vidět, jak se tloušťka osy z, díky perpsektivě, mění.

Trojúhelník není jediné primitivum, které OpenGL umí vykreslit. Zvládne např. i bod, nebo čáru. Čára má ale tu nevýhodu, že na ni nelze aplikovat perspektivu.

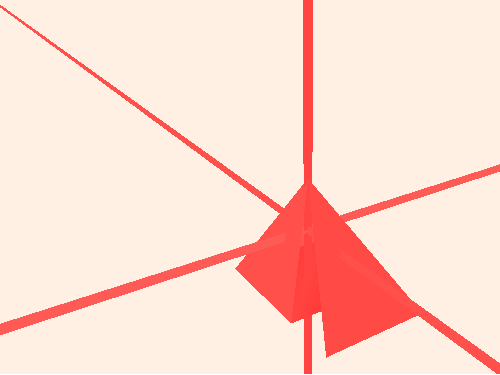
Na druhém obrázku je detail vnitřku jehlanu, kde se osy protínají. Je na něm lépe vidět, že je každá osa tvořena dvěma kolmo se protínajícímí obdélníky.

Každý obdélník je tvořen dvěma trojúhelníky, tj. šesti vrcholy. Trojúhelníky ale některé vrcholy sdílejí, takže by mělo stačit definovat jen čtyři. A pak určit, ze kterých tří vrcholů z těchto čtyř je tvořen jeden trojúhelník a pak ten další.

Pro vykreslení os potřebuji pole vrcholů pro všechny osy (3 osy * 2 obdélníky * 4 vrcholy = 24 vrochlů). A pak, pomocí indexů, určím, kterými vrcholy jsou trojúhelníky tvořeny. Nakonec nesmím zapomenout na barvy vrcholů (taky jich bude 24).

Soubor vertex-data.h jsem rozšířil o proměnné lines, lineIndices a lineColors:

#ifndef  VERTEX_DATA_H
#define VERTEXT_DATA_H
#include <GLFW/glfw3.h>

GLfloat vertices[] = {
        //...
};

GLfloat colors[] = {
         //...
 };
GLfloat lines[]  = {
     -0.09, 100.0,     0.0,
      0.09, 100.0,     0.0,
      0.09,-100.0,     0.0,
    -0.09,-100.0,     0.0,
  -100.0,     .09,    0.0,
   100.0,     .09,    0.0,
   100.0,    -.09,    0.0,
  -100.0,    -.09,    0.0,
      .0,    -.09,  100.0,
      .0,     .09, -100.0,
      .0,    -.09, -100.0,
      .0,     .09,  100.0,
    -0.00, 100.0,   -0.09,
     0.00, 100.0,    0.09,
     0.00,-100.0,    0.09,
    -0.00,-100.0,   -0.09,
  -100.0,     .0,    0.09,
   100.0,     .0,    0.09,
   100.0,     .0,   -0.09,
  -100.0,     .0,   -0.09,
     -.09,    .0,  -100.0,
      .09,    .0,  -100.0,
     -.09,    .0,   100.0,
      .09,    .0,   100.0
};

GLuint lineIndices[] = {
    0, 1, 2, 2, 3, 0,
    4, 5, 6, 6, 7, 4,
    8, 9, 10, 8, 11, 9,
    12, 13, 14, 14, 15, 12,
    16, 17, 18, 18, 19, 17,
    20, 21, 22, 22, 21, 23
};

GLfloat lineColors[] = {
        1.0, 0.0, 0.0, 1.0,
        1.0, 0.0, 0.0, 1.0,
        1.0, 0.0, 0.0, 1.0,
        1.0, 0.0, 0.0, 1.0,
        0.0, 1.0, 0.0, 1.0,
        0.0, 1.0, 0.0, 1.0,
        0.0, 1.0, 0.0, 1.0,
        0.0, 1.0, 0.0, 1.0,
        0.0, 0.0, 1.0, 1.0,
        0.0, 0.0, 1.0, 1.0,
        0.0, 0.0, 1.0, 1.0,
        0.0, 0.0, 1.0, 1.0,
        1.0, 0.0, 0.0, 1.0,
        1.0, 0.0, 0.0, 1.0,
        1.0, 0.0, 0.0, 1.0,
        1.0, 0.0, 0.0, 1.0,
        0.0, 1.0, 0.0, 1.0,
        0.0, 1.0, 0.0, 1.0,
        0.0, 1.0, 0.0, 1.0,
        0.0, 1.0, 0.0, 1.0,
        0.0, 0.0, 1.0, 1.0,
        0.0, 0.0, 1.0, 1.0,
        0.0, 0.0, 1.0, 1.0,
        0.0, 0.0, 1.0, 1.0
};

#endif

Tyto data se zase nahrají do bufferů a nastaví se VAO, tak, jak už to znáte. Jen indexy se nahrají do pole typu GL_ELEMENT_ARRAY_BUFFER místo GL_ARRAY_BUFFER.
Celý trik pak spočívá pouze v tom, že se místo funkce glDrawArrays() zavolá glDrawElements():

glDrawElements(GL_TRIANGLES, sizeof(lineIndices) / sizeof(lineIndices[0]), GL_UNSIGNED_INT, (GLvoid *) 0);

První argument určuje typ primitiva, který se má vykreslit. Druhý argument délku GL_ELEMENT_ARRAY_BUFFERU, resp. počet indexů. Délka může být jiná, například proto, protože indexy nezčínají na začátku bufferu. Kde začínají (jaký je posun od začátku), to určuje poslední argument.

Změny v kódu

Kromě změn ve vertex-data.h popsaných výše budou všechny změny jen v souboru main.c.

Nejdříve je potřeba změnit globální proměnné pro VAO a buffery:

GLuint VAO[2], BO[5];

První VAO budu používat pro vykreslení jehlanu jako v minulé kapitole, druhý VAO pro vykreslení os. Budu také potřebovat další 3 buffery.

Protože budu používat stejný program pro vykreslení os jako pro vykreslení jehlanu, nemusím měnit nic ve vertex ani fragment shaderu, ani např. ve funkci initVariables().
Zato musím změnit funkci initBuffers() – nahrát na grafickou kartu nové vrcholy, indexy a barvy.

void initBuffers(Shader *program)
{
        glGenVertexArrays(2, VAO);
         glGenBuffers(5, BO);
        glBindVertexArray(VAO[0]);
        {
                glBindBuffer(GL_ARRAY_BUFFER, BO[0]);
                glBufferData(GL_ARRAY_BUFFER, sizeof(vertices), vertices, GL_STATIC_DRAW);
                glVertexAttribPointer(0, 3, GL_FLOAT, GL_FALSE, 3 * sizeof(GLfloat), (GLvoid*)0);
                glEnableVertexAttribArray(0);

                glBindBuffer(GL_ARRAY_BUFFER, BO[1]);
                glBufferData(GL_ARRAY_BUFFER, sizeof(colors), colors, GL_STATIC_DRAW);
                glVertexAttribPointer(1, 4, GL_FLOAT, GL_FALSE, 4 * sizeof(GLfloat), (GLvoid*)0);
                glEnableVertexAttribArray(1);
        }
        glBindVertexArray(VAO[1]);
         {
                 glBindBuffer(GL_ARRAY_BUFFER, BO[2]);
                 glBufferData(GL_ARRAY_BUFFER, sizeof(lines), lines, GL_STATIC_DRAW);
                 glVertexAttribPointer(0, 3, GL_FLOAT, GL_FALSE, 3 * sizeof(GLfloat), (GLvoid*)0);
                 glEnableVertexAttribArray(0);
                glBindBuffer(GL_ARRAY_BUFFER, BO[3]);
                 glBufferData(GL_ARRAY_BUFFER, sizeof(lineColors), lineColors, GL_STATIC_DRAW);
                 glVertexAttribPointer(1, 4, GL_FLOAT, GL_FALSE, 4 * sizeof(GLfloat), (GLvoid*)0);
                 glEnableVertexAttribArray(1);
                glBindBuffer(GL_ELEMENT_ARRAY_BUFFER, BO[4]);
                 glBufferData(GL_ELEMENT_ARRAY_BUFFER, sizeof(lineIndices), lineIndices, GL_STATIC_DRAW);
         }
         glBindVertexArray(0); // Unbind VAO
 }

Všiměte si, že indexy se nepředávají do žádné proměnné ve vertex shaderu, takže není potřeba volat glVertexAttribPointer() ani glEneableVertexAttribArray().

Funkce uninitBuffers() se také malinko změnila. Jen maže více VAO a BO:

void uninitBuffers()
{
        glDeleteVertexArrays(2, VAO);
        glDeleteBuffers(4, BO);
}

Poslední změna je ve funkci draw(), kde jsem dal před vykreslování jehlanu vykreslování os:

        // ...

        // Vykresli osy
         glBindVertexArray(VAO[1]);
         glDrawElements(GL_TRIANGLES, sizeof(lineIndices) / sizeof(lineIndices[0]), GL_UNSIGNED_INT, 0);
         glBindVertexArray(0);
        // Vykresli jehlan
        glBindVertexArray(VAO[0]);
        glDrawArrays(GL_TRIANGLES, 0, sizeof(vertices) / sizeof(vertices[0]) / 3);
        glBindVertexArray(0);
 

To je ke kreslení os a optimalizaci pomocí glDrawArrays() vše.

Kamera

Teď zpět k příkladu s kamerou.

Z kódu příkladu s jehlanem z minulé kaptioly jsem odstranil rPyramdid a vše, co s otáčením souviselo. Naopak jsem přidal kód do funkce draw(), který se stará o transformaci světa (celý svět se transformuje tak, aby to vypadalo, jako že se pousová místo a směr kamery).

        mat4x4 uMVMatrix, uPMatrix, uViewMatrix;
       
        vec3 targetPosition = { 0.0, 0.0, -5.0 };
        mat4x4_perspective(uPMatrix, degToRad(45.0), ((GLfloat)width) / height, 1.0, 100.0);
        mat4x4_translate(uMVMatrix, targetPosition[0], targetPosition[1], targetPosition[2]);
         mat4x4_translate(uViewMatrix, cameraPos.x, cameraPos.y, cameraPos.z);
         mat4x4_invert(uViewMatrix, uViewMatrix);
         mat4x4_mul(uMVMatrix, uViewMatrix, uMVMatrix);

Kód nejdříve přesouvá jehlan na targetPosition. To je úvodní pozice jehlanu. Následně se nastaví view matrix podle pozice struktury cameraPos a tato pozice se invertuje (protože posun kamery vpřed se simuluje posunem celého světa vzad atd.). Nakonec se view matrix aplikuje se na uMVmatrix.

To je k popisu kamery vlastně vše. Už jen zbývá zodpovědět otázku, kde se vezme struktura cameraPos a jak se mění její složky x,y a z.

Tato struktura je definovaná v souboru events.h, kde je i definovaná funkce pro obsluhu události klávesnice key_callback(), jež hodnoty členů struktury cameraPos mění.

struct {
        float x;
        float y;
        float z;
} cameraPos = { 0.0, 0.0, 5.0 };

static void key_callback(GLFWwindow* window, int key, int scancode, int action, int mods)
{
        if (key == GLFW_KEY_ESCAPE && action == GLFW_PRESS) {
                glfwSetWindowShouldClose(window, GLFW_TRUE);
                return;
        }
        if(action != GLFW_PRESS) {
                return;
        }
        GLfloat delta = 0.5;
        if(key == GLFW_KEY_LEFT) cameraPos.x -= delta;
        else if(key == GLFW_KEY_RIGHT) cameraPos.x += delta;
        else if(key == GLFW_KEY_DOWN) cameraPos.z -= delta;
        else if(key == GLFW_KEY_UP) cameraPos.z += delta;
        else if(key == GLFW_KEY_S) cameraPos.y += delta;
        else if(key == GLFW_KEY_X) cameraPos.y -= delta;
}

void mouse_button_callback(GLFWwindow* window, int button, int action, int mods)
{
}

Z kódu je jasné, že k změně pozice kamery můžete používat šipky na klávesnici a znaky S a X.

Look At

Poslední problém řešený touto kapitolou je použití funkce lookAt().

Zdrojový kód se bude oproti příkladu výše lišit jen ve funkci draw() a to na místě, kde se nastavují matice transformace.

        // ...
        mat4x4 uMVMatrix, uPMatrix, uViewMatrix;

        mat4x4_perspective(uPMatrix, degToRad(45.0), ((GLfloat)width) / height, 1.0, 100.0);

        vec3 targetPosition = { 0.0, 0.0, -5.0 };
        mat4x4_translate(uMVMatrix, targetPosition[0], targetPosition[1], targetPosition[2]);

        vec3 upVector = { 0.0, 1.0, 0.0 };
         if (cameraPos.x == 0.0 && cameraPos.z == -5.0) {
                 upVector[1] = .0; upVector[2] = 1.0;
         }
         mat4x4_translate(uViewMatrix, cameraPos.x, cameraPos.y, cameraPos.z);
         mat4x4_look_at(uViewMatrix, (float *)&cameraPos, targetPosition, upVector);
         mat4x4_mul(uMVMatrix, uViewMatrix, uMVMatrix);
        glUniformMatrix4fv(variables.uMVMatrixLoc, 1, GL_FALSE, (const GLfloat *)uMVMatrix);
        glUniformMatrix4fv(variables.uPMatrixLoc, 1, GL_FALSE, (const GLfloat *)uPMatrix);
        // ...

Funkce mat4x4_look_at() inicializuje matici pohledu uViewMatrix. Potřebuje k tomu znát pozici kamery (cameraPos), pozici, kam se má dívat (targetPosition) a vektor, kteý směřuje nahoru (upVector).

Jak bylo popsáno v kapitole o kameře, pro orientaci v prostoru jsou potřeba 3 kolmé vektory. Třetí se dá spočítat na základě prvních dvou (vektoru upVector a vektoru mezi cameraPos a targetPosition).

To ale funguje jen v případě, že tyto dva vektory nejsou rovnoběžné. Vektor upVector směřuje podél osy y. Proto je ve funkci draw() podmínka, která ve chvíli, kdy by směr od cameraPos k targetPosition také směřoval podél osy y, upVektror nasměruje podél osy z. Hrubé, ale funguje to.

Není stále vyřešen jeden problém, a to, když se přesune cameraPos do místa targetPosition. V takovou chvíli se stane vektor určující směr mezi těmito body nulový a funkce mat4x4_look_at() přestane fungovat.

Zmíněné řešení zmíněných problémů není jediné možné a správné. Mělo by vám dát jen představu o tom, jak funkce „look at“ funguje. V tomto tutoriálu vás ještě čeká jedna kapitola, kde uvidíte, jak vytvořit kameru alá FPS. (Kapitola o pohybu.)

Závěr

V této kapitole jste se naučili, jak použít element array pro optimalizaci objemu dat potřebného pro popis objektu. Je to velmi často používaná technika, takže ji určitě neopomíjejte.

Také jste mohli vidět, jak použít klávesnici pro „pohyb v prostoru“, a v neposlední řadě jak použít funkci „look at“ pro pohled určitým zadaným směrem.

Komentář Hlášení chyby
Created: 24.12.2016
Last updated: 24.11.2017
Tato stánka používá ke svému běhu cookies, díky kterým je možné monitorovat, co tu provádíte (ne že bych to bez cookies nezvládl). Také vás tu bude špehovat google analytics. Jestli si myslíte, že je to problém, vypněte si cookies ve vašem prohlížeči, nebo odejděte a už se nevracejte :-). Prohlížením tohoto webu souhlasíte s používáním cookies. Dozvědět se více..